En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra 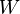 (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
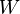 (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
Ya que por definición el trabajo es un tránsito de energía, nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.
El trabajo en mecánica
Consideremos una partícula  sobre la que actúa una fuerza
sobre la que actúa una fuerza  , función de la posición de la partícula en el espacio, esto es
, función de la posición de la partícula en el espacio, esto es  y sea
y sea  un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo
un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo  . Llamamos trabajo elemental,
. Llamamos trabajo elemental,  , de la fuerza
, de la fuerza  durante el desplazamiento elemental
durante el desplazamiento elemental  al producto escalar
al producto escalar  ; esto es,
; esto es,
 sobre la que actúa una fuerza
sobre la que actúa una fuerza  , función de la posición de la partícula en el espacio, esto es
, función de la posición de la partícula en el espacio, esto es  y sea
y sea  un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo
un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo  . Llamamos trabajo elemental,
. Llamamos trabajo elemental,  , de la fuerza
, de la fuerza  durante el desplazamiento elemental
durante el desplazamiento elemental  al producto escalar
al producto escalar  ; esto es,
; esto es,
Si representamos por  la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es
la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es  , entonces el vector tangente a la trayectoria viene dado por
, entonces el vector tangente a la trayectoria viene dado por 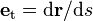 y podemos escribir la expresión anterior en la forma
y podemos escribir la expresión anterior en la forma
 la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es
la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es  , entonces el vector tangente a la trayectoria viene dado por
, entonces el vector tangente a la trayectoria viene dado por 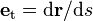 y podemos escribir la expresión anterior en la forma
y podemos escribir la expresión anterior en la forma
donde  representa el ángulo determinado por los vectores
representa el ángulo determinado por los vectores 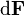 y
y  y
y 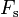 es la componente de la fuerza F en la dirección del desplazamiento elemental
es la componente de la fuerza F en la dirección del desplazamiento elemental  .
.
 representa el ángulo determinado por los vectores
representa el ángulo determinado por los vectores 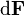 y
y  y
y 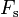 es la componente de la fuerza F en la dirección del desplazamiento elemental
es la componente de la fuerza F en la dirección del desplazamiento elemental  .
.El trabajo realizado por la fuerza
 durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo
durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo  sea agudo, recto u obtuso.
sea agudo, recto u obtuso.
Si la partícula P recorre una cierta trayectoria en el espacio, su desplazamiento total entre dos posiciones A y B puede considerarse como el resultado de sumar infinitos desplazamientos elementales  y el trabajo total realizado por la fuerza
y el trabajo total realizado por la fuerza  en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
 y el trabajo total realizado por la fuerza
y el trabajo total realizado por la fuerza  en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
Esto es, el trabajo viene dado por la integral curvilínea de  a lo largo de la curva
a lo largo de la curva  que une los dos puntos; en otras palabras, por la circulación de
que une los dos puntos; en otras palabras, por la circulación de  sobre la curva
sobre la curva  entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza
entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza  sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
 a lo largo de la curva
a lo largo de la curva  que une los dos puntos; en otras palabras, por la circulación de
que une los dos puntos; en otras palabras, por la circulación de  sobre la curva
sobre la curva  entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza
entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza  sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.Casos particulares
- Fuerza constante sobre una partícula
En el caso particular de que la fuerza aplicada a la partícula sea constante (en módulo, dirección y sentido), se tiene que
es decir, el trabajo realizado por una fuerza constante viene expresado por el producto escalar de la fuerza por el vector desplazamiento total entre la posición inicial y la final. Cuando el vector fuerza es perpendicular al vector desplazamiento del cuerpo sobre el que se aplica, dicha fuerza no realiza trabajo alguno. Asimismo, si no hay desplazamiento, el trabajo también será nulo.
Si sobre una partícula actúan varias fuerzas y queremos calcular el trabajo total realizado sobre esta ella, entonces  representará al vector resultante de todas las fuerzas aplicadas.
representará al vector resultante de todas las fuerzas aplicadas.
 representará al vector resultante de todas las fuerzas aplicadas.
representará al vector resultante de todas las fuerzas aplicadas.- Trabajo sobre un sólido rígido
Para el caso de un sólido el trabajo total sobre el mismo se calcula sumando las contribuciones sobre todas las partículas. Matemáticamente ese trabajo puede expresarse como integral:
Si se trata de un sólido rígido las fuerzas de volumen  puede escribirse en términos de la fuerza resultante
puede escribirse en términos de la fuerza resultante  , el momento resultante
, el momento resultante  , la velocidad del centro de masas
, la velocidad del centro de masas  y la velocidad angular
y la velocidad angular  :
:
 puede escribirse en términos de la fuerza resultante
puede escribirse en términos de la fuerza resultante  , el momento resultante
, el momento resultante  , la velocidad del centro de masas
, la velocidad del centro de masas  y la velocidad angular
y la velocidad angular  :
:Trabajo y energía cinética
Para el caso de una partícula tanto en mecánica clásica como en mecánica relativista es válida la siguiente expresión:
Multiplicando esta expresión escalarmente por la velocidad e integrando respecto al tiempo se obtiene que el trabajo realizado sobre una partícula (clásica o relativista) iguala a la variación de energía cinética:
El trabajo en termodinámica
En el caso de un sistema termodinámico, el trabajo no es necesariamente de naturaleza puramente mecánica, ya que la energía intercambiada en las interacciones puede ser también calorífica, eléctrica, magnética o química, por lo que no siempre podrá expresarse en la forma de trabajo mecánico.
No obstante, existe una situación particularmente simple e importante en la que el trabajo está asociado a los cambios de volumen que experimenta un sistema (v.g., un fluido contenido en un recinto de forma variable).
Así, si consideramos un fluido que se encuentra sometido a una presión externa 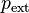 y que evoluciona desde un estado caracterizado por un volumen
y que evoluciona desde un estado caracterizado por un volumen 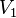 a otro con un volumen
a otro con un volumen 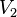 , el trabajo realizado será:
, el trabajo realizado será:
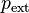 y que evoluciona desde un estado caracterizado por un volumen
y que evoluciona desde un estado caracterizado por un volumen 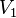 a otro con un volumen
a otro con un volumen 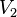 , el trabajo realizado será:
, el trabajo realizado será:
resultando un trabajo positivo ( ) si se trata de una expansión del sistema
) si se trata de una expansión del sistema  y negativo en caso contrario, de acuerdo con el convenio de signos aceptado en la Termodinámica. En un proceso cuasiestático y sin fricción la presión exterior (
y negativo en caso contrario, de acuerdo con el convenio de signos aceptado en la Termodinámica. En un proceso cuasiestático y sin fricción la presión exterior ( ) será igual en cada instante a la presión (
) será igual en cada instante a la presión ( ) del fluido, de modo que el trabajo intercambiado por el sistema en estos procesos se expresa como
) del fluido, de modo que el trabajo intercambiado por el sistema en estos procesos se expresa como
 ) si se trata de una expansión del sistema
) si se trata de una expansión del sistema  y negativo en caso contrario, de acuerdo con el convenio de signos aceptado en la Termodinámica. En un proceso cuasiestático y sin fricción la presión exterior (
y negativo en caso contrario, de acuerdo con el convenio de signos aceptado en la Termodinámica. En un proceso cuasiestático y sin fricción la presión exterior ( ) será igual en cada instante a la presión (
) será igual en cada instante a la presión ( ) del fluido, de modo que el trabajo intercambiado por el sistema en estos procesos se expresa como
) del fluido, de modo que el trabajo intercambiado por el sistema en estos procesos se expresa como
De estas expresiones se infiere que la presión se comporta como una fuerza generalizada, en tanto que el volumen actúa como un desplazamiento generalizado; la presión y el volumen constituyen una pareja de variables conjugadas.
En el caso que la presión del sistema permanezca constante durante el proceso, el trabajo viene dado por:


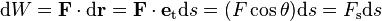
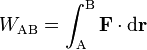

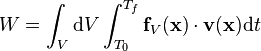







No hay comentarios.:
Publicar un comentario