La temperatura de un gas ideal monoatómico es una medida relacionada con la energía cinética promedio de sus moléculas al moverse. En esta animación, se muestra a escala la relación entre el tamaño de los átomos de helio respecto a su espaciado bajo una presión de 1950 atmósferas. Estos átomos, a temperatura ambiente, muestran una velocidad media que en esta animación se ha reducido dos
billones de veces. De todas maneras, en un instante determinado, un átomo particular de helio puede moverse mucho más rápido que esa velocidad media mientras que otro puede permanecer prácticamente inmóvil.
La
temperatura es una magnitud referida a las nociones comunes de calor medible mediante un termómetro. En física, se define como una magnitud escalar relacionada con la energía interna de un sistema termodinámico, definida por el principio cero de la termodinámica. Más específicamente, está relacionada directamente con la parte de la energía interna conocida como «energía cinética», que es la energía asociada a los movimientos de las partículas del sistema, sea en un sentido traslacional, rotacional, o en forma de vibraciones. A medida de que sea mayor la energía cinética de un sistema, se observa que éste se encuentra más «caliente»; es decir, que su temperatura es mayor.
En el caso de un sólido, los movimientos en cuestión resultan ser las vibraciones de las partículas en sus sitios dentro del sólido. En el caso de un gas ideal monoatómico se trata de los movimientos traslacionales de sus partículas (para los gases multiatómicos los movimientos rotacional y vibracional deben tomarse en cuenta también).
El desarrollo de técnicas para la medición de la temperatura ha pasado por un largo proceso histórico, ya que es necesario darle un valor numérico a una idea intuitiva como es lo frío o lo caliente.
Multitud de propiedades fisicoquímicas de los materiales o las sustancias varían en función de la temperatura a la que se encuentren, como por ejemplo su estado (sólido, líquido, gaseoso, plasma), su volumen, la solubilidad, la presión de vapor, su color o la conductividad eléctrica. Así mismo es uno de los factores que influyen en la velocidad a la que tienen lugar las reacciones químicas.
La temperatura se mide con termómetros, los cuales pueden ser calibrados de acuerdo a una multitud de escalas que dan lugar a unidades de medición de la temperatura. En el Sistema Internacional de Unidades, la unidad de temperatura es el kelvin (K), y la escala correspondiente es la escala Kelvin o escala absoluta, que asocia el valor «cero kelvin» (0 K) al «cero absoluto», y se gradúa con un tamaño de grado igual al del grado Celsius. Sin embargo, fuera del ámbito científico el uso de otras escalas de temperatura es común. La escala más extendida es la escala Celsius, llamada «centígrada»; y, en mucha menor medida, y prácticamente solo en los Estados Unidos, la escala Fahrenheit. También se usa a veces la escala Rankine (°R) que establece su punto de referencia en el mismo punto de la escala Kelvin, el cero absoluto, pero con un tamaño de grado igual al de la Fahrenheit, y es usada únicamente en Estados Unidos, y solo en algunos campos de la ingeniería.
Escalas Termométricas
Para que seja possível medir a temperatura de um corpo, foi desenvolvido
um aparelho chamado termômetro.
O termômetro mais comum é o de mercúrio, que consiste em um vidro
graduado com um bulbo de paredes finas que é ligado a um tubo muito fino,
chamado tubo capilar.
Quando a temperatura do termômetro aumenta, as moléculas de mercúrio
aumentam sua agitação fazendo com que este se dilate, preenchendo o tubo
capilar. Para cada altura atingida pelo mercúrio está associada uma
temperatura.
A escala de cada termômetro corresponde a este valor de altura atingida.
Escala Celsius
É a escala usada no Brasil e na maior parte dos países, oficializada em
1742 pelo astrônomo e físico sueco Anders Celsius (1701-1744). Esta escala tem
como pontos de referência a temperatura de congelamento da água sob pressão
normal (0 °C) e a temperatura de ebulição da água sob pressão normal (100 °C).
Escala Fahrenheit
Outra escala bastante utilizada, principalmente nos países de língua
inglesa, criada em 1708 pelo físico alemão Daniel Gabriel Fahrenheit
(1686-1736), tendo como referência a temperatura de uma mistura de gelo e
cloreto de amônia (0 °F) e a temperatura do corpo humano (100 °F).
Em comparação com a escala Celsius:
0 °C = 32 °F
100 °C = 212 °F
Escala Kelvin
Também conhecida como escala absoluta, foi verificada pelo físico inglês
William Thompson (1824-1907), também conhecido como Lorde Kelvin. Esta escala
tem como referência a temperatura do menor estado de agitação de qualquer
molécula (0 K) e é calculada apartir da escala Celsius.
Por convenção, não se usa "grau" para esta escala, ou seja 0
K, lê-se zero kelvin e não zero grau kelvin. Em comparação com a escala
Celsius:
-273 °C = 0 K
0 °C = 273 K
100 °C = 373 K
TERMOMETRIA Y SUS DIFERENTES ESCALAS
La termometría se encarga de la
medición de la temperatura de cuerpos o sistemas.
Existen
varias escalas termométricas para medir temperaturas, relativas
(específicas) y absolutas.
A partir de la sensación
fisiológica, es posible hacerse una idea aproximada de la temperatura a la que
se encuentra un objeto. Pero esa apreciación directa está limitada por
diferentes factores. Por ello para medir temperaturas se recurre a los
termómetros.
En el sistema SI de
unidades, las unidades más utilizada para medir la temperatura son la Celsius
(° C) y el sistema Inglés utiliza la escala Fahrenheit (F); estas en la
escala específica. Hay también la escala de temperaturas absolutas, Kelvin
(K) y Rankine.
Hasta 1954 estas escalas
termométricas se basan en la fusión del hielo y el agua hirviendo. La
temperatura de fusión del hielo se define como la temperatura de una mezcla de
hielo y agua, en la escala específica recibe la marca 0 ° centígrados y 32
°F. La temperatura de vaporización del agua es la temperatura a la cual el
agua y el vapor están en equilibrio a la presión de 1 atm; en la escala
específica recibe la marca de los 100 ° centígrados 212 °F.
La escala Kelvin es la
escala de temperatura absoluta que se relaciona con la escala Celsius. Esta
relación es la siguiente:
Siendo 273,15 K a la
fusión del hielo y K 373,15 para hervir agua.
La escala de Rankine es la escala de temperatura absoluta que se relaciona con
la escala Fahrenheit, y esto se lleva a cabo de la siguiente manera:
Siendo R 491,67 por
derretimiento del hielo y R 671,67 por agua hirviendo.
Escala Celsius
El científico
sueco Anders Celsius (1701-1744) construyó por primera vez la escala
termométrica que lleva su nombre. Eligió como puntos fijos el de fusión del
hielo y el de ebullición del agua.
Asignó al primero el
valor 0 y al segundo el valor 100, con lo cual fijó el valor del grado Celsius
(°C) como la centésima parte del intervalo de temperatura comprendido entre
esos dos puntos fijos.
Celsius definió su
escala en 1742 considerando las temperaturas de congelación y ebullición del
agua, asignándoles originalmente los valores 0 °C y 100 °C
respectivamente (de manera que más caliente resultaba en
una menor temperatura); fue Carlos Linneo quien invirtió ambos
puntos un par de años más tarde.
William
Thomson definió en 1848 su escala absoluta de temperatura en
términos del grado Celsius.
La escala de Celsius es
muy utilizada para expresar las temperaturas de uso cotidiano, desde la
temperatura del aire a la de un sin fin de dispositivos domésticos.
También se la utiliza en
trabajos científicos y tecnológicos, aunque en muchos casos resulta obligada la
utilización de la escala de Kelvin.
Escala Fahrenheit
El grado Fahrenheit (representado como °F) es una escala de temperatura
propuesta por Daniel Gabriel Fahrenheit en 1714. La escala establece como las
temperaturas de congelación y evaporación del agua, 32 °F y 212 °F,
respectivamente. El método de definición es similar al utilizado para el grado
Celsius (°C).
Esta escala divide la diferencia entre los puntos de fusión y de ebullición
del agua en 180 intervalos iguales.
Escala Kelvin
Si bien en la vida
diaria las escalas Celsius y Fahrenheit son las más importantes, en ámbito
científico se usa otra, llamada "absoluta" o Kelvin, en honor a sir
Lord Kelvin.
El kelvin, simbolizado
como K, es la unidad de temperatura de la escala creada por William Thomson en
el año 1848, sobre la base del grado Celsius.
Se representa con la
letra K, y nunca "°K". Actualmente, su nombre no es el de
"grados kelvin", sino simplemente "kelvin".
Coincidiendo el
incremento en un grado Celsius con el de un kelvin, su importancia radica en el
0 de la escala: la temperatura de 0 K es denominada 'cero absoluto' y
corresponde al punto en el que las moléculas y átomos de un sistema tienen la
mínima energía térmica posible.
También en iluminación
de vídeo y cine se utilizan los kelvin como referencia de la temperatura de
color.
Escala Rankine
Se denomina Rankine a la
escala de temperatura que se define midiendo en grados Fahrenheit sobre el cero
absoluto, por lo que carece de valores negativos. Esta escala fue propuesta por
el físico e ingeniero escocés William Rankine en 1859.
El grado Rankine tiene
su punto de cero absoluto a −459,67°F y los intervalos de grado son idénticos
al intervalo de grado Fahrenheit.
Usado comúnmente en
EE.UU. como medida de temperatura termodinámica. Aunque en la comunidad
científica las medidas son efectuada en Sistema Internacional de Unidades, por
tanto la temperatura es medida en Kelvin (K).
El grado Rankine tiene
su punto de cero absoluto a −459,67°F y los intervalos de grado son idénticos
al intervalo de grado Fahrenheit. La relación entre la temperatura en grados
Rankine (R) y la temperatura correspondiente en grados (°F) Fahrenheit es:
R=F+459.67
F=R-459.67
Cero grados Rankine (0 °R) equivalen a −273,15 °C ó 0 K. Para convertir de grados
Rankine a Kelvin se multiplica por un factor de 9/5:
R=9/5K
K=5/9R
R=9/5C+491.67
C=5/9R-273.15

 , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 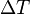 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
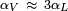 , es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
, es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.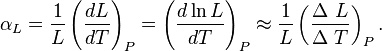
![L_f = L_0 [1 +\alpha_L (T_f - T_0)]\;](https://upload.wikimedia.org/math/4/d/8/4d8d9e521d59aa36de0d776706db3b16.png)
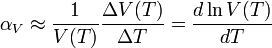


![A_f = A_0 [1 +\gamma_A (T_f - T_0)]\;](https://upload.wikimedia.org/math/8/4/4/84444b9c6e865aaf0b6d1376be7a9a6b.png)


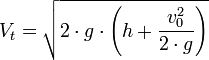
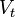 es la velocidad teórica del líquido a la salida del orificio
es la velocidad teórica del líquido a la salida del orificio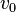 es la velocidad de aproximación o inicial.
es la velocidad de aproximación o inicial.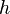 es la distancia desde la superficie del líquido al centro del orificio.
es la distancia desde la superficie del líquido al centro del orificio.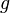 es la aceleración de la gravedad
es la aceleración de la gravedad
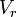 es la velocidad real media del líquido a la salida del orificio
es la velocidad real media del líquido a la salida del orificio es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
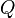 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 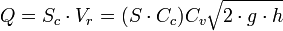
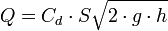
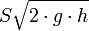 representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.
representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.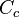 es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída
es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída 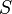 . Suele estar en torno a 0,65.
. Suele estar en torno a 0,65.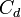 es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes.
es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes. 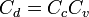



 =
=  =
=  =
=  =
=  = altura en la dirección de la
= altura en la dirección de la  (donde
(donde  ) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[
) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[
 , de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.




 es una constante-
es una constante-

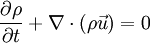
 es la densidad, t el tiempo y
es la densidad, t el tiempo y 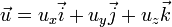 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.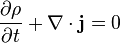
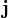 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
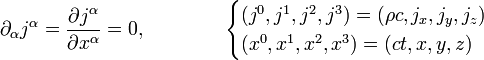
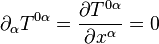
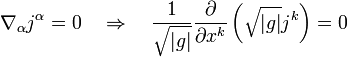
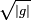 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía: